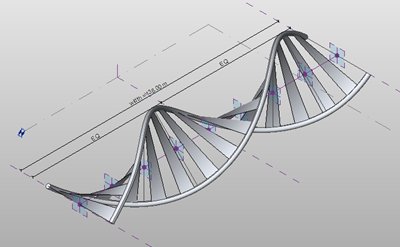
This post comes from experimenting with hosted points on lines and arcs and attempting to create a helical form in the massing environment similar to Zach Kron’s recent post. I guessed that you could do something similar using lines connected to hosted points on circles.
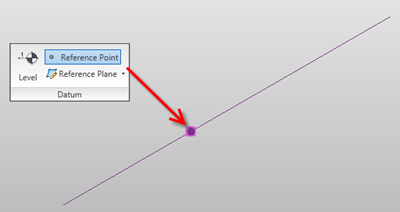
So let go back to basics. Points can be hosted to lines, arcs, splines, circles and ellipses (either reference line or lines). Just draw a line or reference line then choose the point tool and place the point on the line. It will snap to the line and you will notice it will change in size and will now include a work plane.
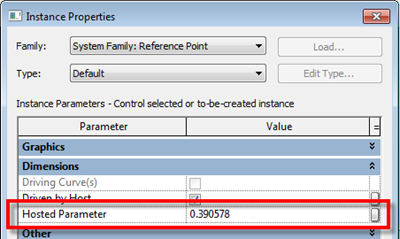
If you select the point and choose properties, you will discover that there is now a hosted parameter. This parameter drives the position of the point and it goes from 0 to 1. “0” being one end and “1” the other end. If you wanted to place the point half way along the line, plug in 0.5, voila the point is position half way along the line.
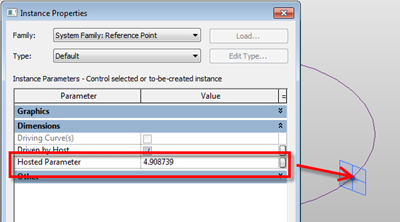
So lines are straight forward, what about circles or even ellipses? Hmmmmm Ok, go ahead do the same thing, but this time draw a circle as a line or reference line and place a point on the circle. Go check the properties of the Hosted Parameter…. No 0 to 1???? some other weird combination of figures????!!!
So what’s going on here? Well I’m no mathematician, so after a bit of investigation I discovered that points are managed differently on closed elements such as circles. You need to go back to do some math…
So the hosted parameter value for a circle is 2pi
(where pi is 3.1415926535897932384626433832795)
therefore 2 x 3.141593 is equal to 6.283186 radians
So the hosted point can have a value between 0 to 6.28318 depending on where it is on the circle.
So to split the circle into degrees
1 degree=2pi/360=0.017453 radians
With this logic in mind try this, create a circle in the massing environment and host a point on the circle. Go the the hosted parameters, then plug in the following figures and watch the position of the points change.
- 0 degrees - 0 x 0.017453 = 0
- 90 degrees – 90 x 0.017453 = 1.570796
- 180 degrees – 180 x 0.017453 = 3.141593
- 270 degrees – 270 x 0.017453 = 4.712389
- 360 degrees – 360 x 0.017453 = 6.28308
This opens up to interesting opportunities and allowed me to create the helix using points and lines along with nested families. I’ll show you how I did this in another post……